Lista Número 1
Exercícios do Capítulo I: "Análise Exploratória Geoestatística", do livro "Introdução à geoestatística Com programas em R". Data de entrega: 29/08/2019.
Exercício 1
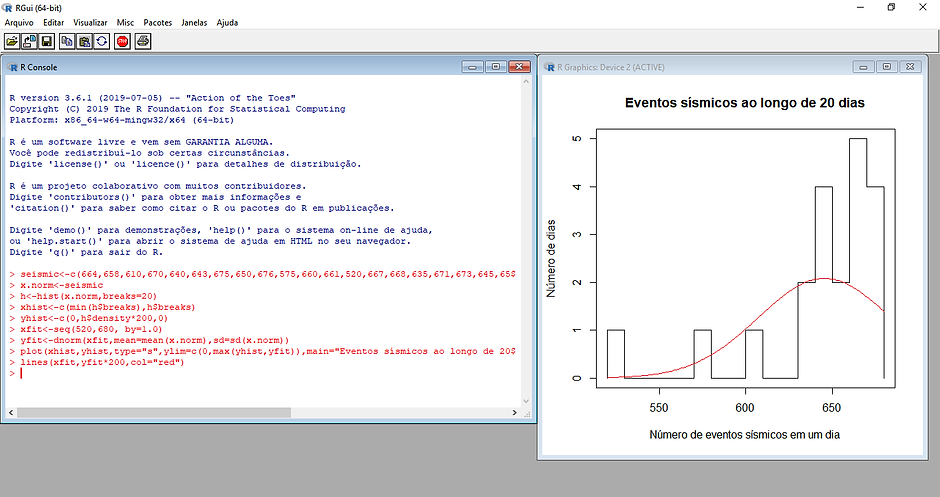
Após a plotagem do gráfico e da curva normal ajustada, podemos concluir que o padrão destes valores é assimétrico à esquerda. Portanto, a resposta correta é a letra b).
Exercício 4
Para se calcular o aumento médio anual, devemos encontrar a média geométrica.
No primeiro ano, o montante final foi de 2,1 vezes o inicial. Já no segundo ano, o montante final foi de 2,5 vezes o montante do ano anterior. Multiplicando-se os dois números,
obtemos: 2,1 * 2,5 = 5,25. A raiz quadrada deste resultado é 2,29 aproximadamente.
Se para cada ano o montante final é de 2,29 vezes o montante inicial, o aumento médio anual é de 129%.
Exercício 5
Em um primeiro momento, a melhor opção de investimento parece ser a mais conservadora, visto que há um maior retorno devido à chance maior de se ganhar dinheiro. Entretanto, investidores possuem um montante inicial que os permite arcar com perdas no início de um investimento, se isso significar que o lucro virá a longo prazo. Portanto, quanto mais investimentos forem feitos, maior será a tendência das chances percentuais se alinharem como o esperado. Considerando então um caso em que são feitos muitos investimentos, a média de lucro em cada investimento pode ser calculada da seguinte maneira:
1º Caso: R$ 250.000.000,00 * 0,1 - R$ 10.000.000,00 * 0,9 = R$ 16.000.000,00
2º Caso: R$ 40.000.000,00 * 0,5 - R$ 2.000.000,00 * 0,5 = R$ 19.000.000,00
3º Caso: R$ 800.000.000,00 * 0,05 - R$ 20.000.000,00 * 0,95 = R$ 21.000.000,00
Conclui-se então que o 3º caso (coincidentemente o mais arriscado) gerará o maior lucro.
Exercício 6
A distância entre os pontos A e B é de 30 Km. A ida AB foi feita na velocidade de 10 Km/h, enquanto que a volta BA foi feita na velocidade de 30 Km/h. Para calcular a velocidade média, basta somar a distância total percorrida pelo tempo que a ida e a volta tomaram.
A ida AB levou:
30 Km/10 Km/h = 3 h
Já a volta BA levou:
30 Km/30 Km/h = 1 h
O tempo total foi de 4 h e a distância percorrida é de 30 Km * 2 = 60 Km
A velocidade média em todo o percurso é de:
60 Km / 4 h
=
15 Km/h
Exercício 7
Dados iniciais:
k1 = 10 mD; k2 = 12 mD; k3 = 15 mD
h1 = 10 cm; h2 = 20 cm; h3 = 30 cm; W = 40 cm; L = 60 cm
Para se achar ki, consideramos que Qt = ki * At
Logo, ki = Qt / At
Qt = Q1 + Q2 + Q3
Qt = k1A1 + k2A2 + k3A3
ki = (k1A1 + k2A2 + k3A3) / At
A1 = W * h1 = 400 cm; A2 = W * h2 = 800 cm; A3 = W * h3 = 1200 cm;
At = A1 + A2 + A3 = 2400 cm
Ki = (10 * 400 + 12 * 800 + 15 * 1200) / 2400
Ki = 31600 / 2400
Ki = 13,16 mD
Exercício 8
Dados iniciais:
k1 = 10 mD; k2 = 12 mD; k3 = 15 mD
L1 = 10 cm; L2 = 20 cm; L3 = 30 cm; W = 40 cm; L = 60 cm
Para se encontrar o ki em um fluxo vertical, nos utilizamos da fórmula: K = L/(Li/Ki), onde Li/Ki é o somatório L1/k1 + L2/k2 + L3/k3.
Li/Ki = 10/10 + 20/12 + 30/15 = 1 + 1,67 + 2 = 4,67
K = L / 4,67 = 60 / 4,67
K = 12,84 mD
Exercício 9
No caso observado neste exercício, temos a seguinte amostra:
[21,5 21,5 22,5 22,5 22,5 23,5 24,5 25,5 26,5 27,5]
São então 10 valores no total, portanto, N = 10.
Calculando cada quartil:
Q1 = número na posição (N+1)*0,25
Q1 = 11*0,25 = 2,75
Arredondando, temos que o termo 3 será o 1º quartil. Logo, Q1 = 22,5.
Como N é par, Q2 = [(N/2)+(N/2)+1]/2
Q2 = (termo 5+termo 6)]/2
Q2 = (22,5 + 23,5)/2 = 23.
Q3 = número na posição (N+1)*0,75
Q3 = 11*0,75 = 8,25
Arredondando, temos que o termo 8 será o 1º quartil. Logo, Q3 = 25,5.
Resposta Final: Q1 = 22,5; Q2 = 23; Q3 = 25,5.
Exercício 10
Considere que r é o coeficiente de correlação das variáveis. Quanto mais próximos de uma curva de coeficiente angular 1, maior será o coeficiente de correlação.
Com base nos três casos apresentados, podemos observar que r1 e r2 são negativos, porém, r1 é um pouco maior que r2, já que na curva de r1 pelo menos dois valores seguem uma curva de coef. angular > 0. Podemos assim que concluir que r1 < 0, r2 < 0, r3 = 0, r1 < r2.
A resposta correta então será a letra b) r2 < r1 < r3.
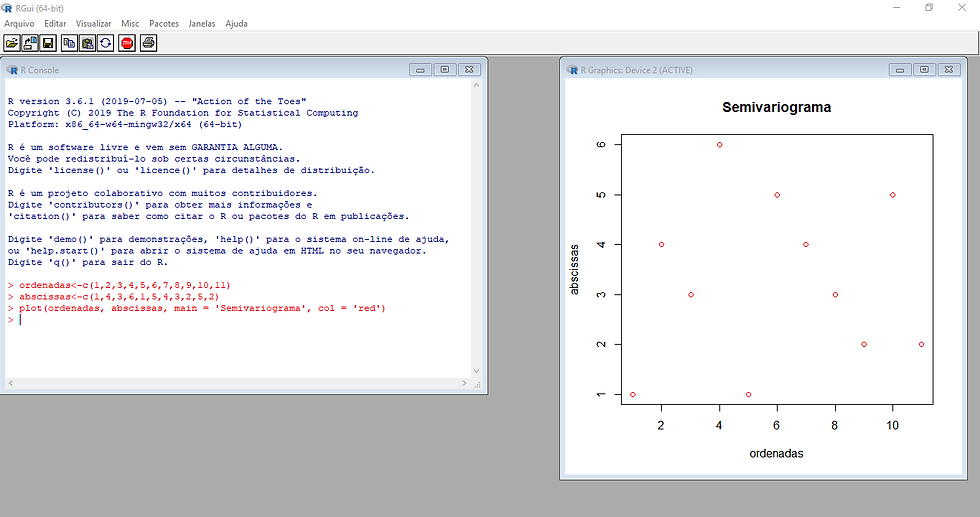
Exercício 11
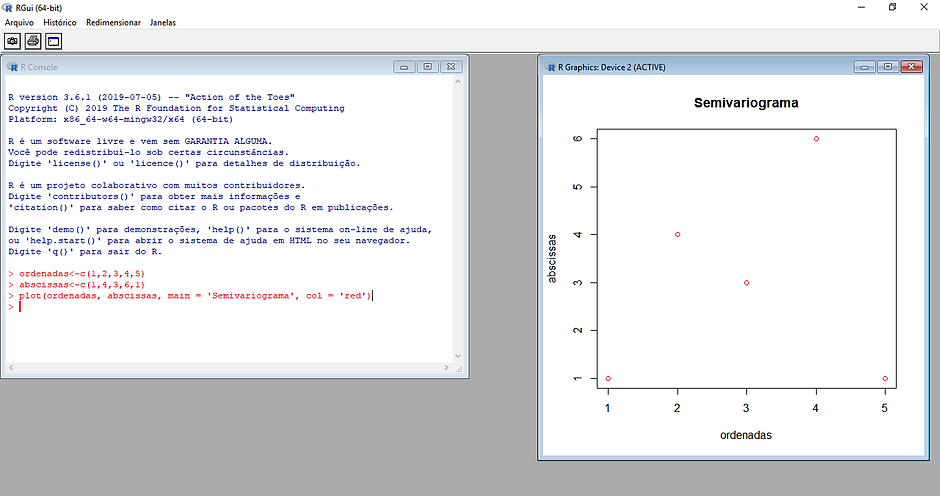
É possível ver o semivariograma experimental na imagem abaixo, após o mesmo ter sido plotado em R.
Exercício 12
No primeiro estudo, por se tratar apenas de uma análise imparcial de dados coletados após um intervalo de tempo, os resultados não sofreram intervenção nem viés algum. O estudo pode ser classificado como observacional.
Já no segundo estudo, os resultados obtidos sofreram uma alteração em função do treinamento do qual os participantes foram submetidos. Esta intervenção provoca causa portanto um impacto no estudo, sendo portanto classificado como um experimento controlado.
A resposta correta é a letra b).
Exercício 13
O número de vezes que uma amostra estratificada pode ser extraída está especificado na imagem abaixo:
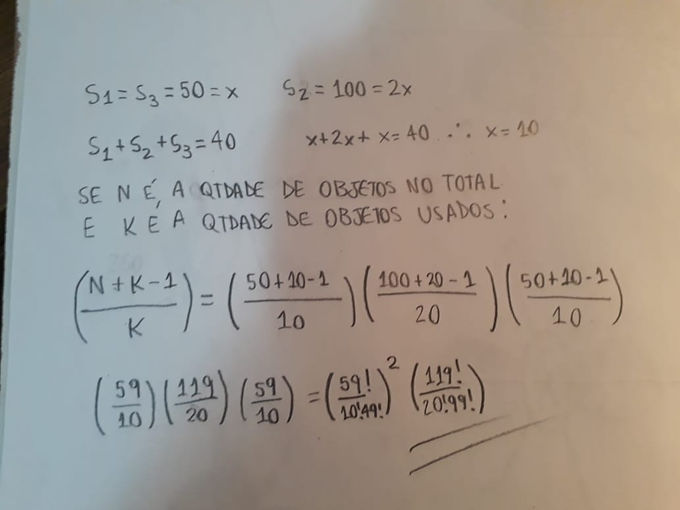
Exercício 14
Item a) Convertendo-se a média de Celsius para Kelvin, basta somar 273,16 ao valor inicial. Teremos portanto:
Média em Kelvin = 25,32 + 273,16 = 298,48 K.
Com relação ao valor de desvio padrão, o mesmo não sofrerá alteração, já que o desvio padrão é uma estatística que não depende do valor absoluto da unidade amostral, mas sim da distribuição das variáveis de uma amostra ( que não se altera ao se somar um valor igual para todas as unidades amostrais).
O desvio padrão em Kelvin será então de 4,7 K.
Item b) Similarmente ao item a), basta multiplicar a média amostral pela constante 2,471 para que obtenhamos o novo valor de média amostral:
Média em acres = 59,2 * 2,471 = 146,28 acres.
No entanto, para o desvio padrão, por se tratar de uma operação de multiplicação, não podemos fazer a mesma operação que no item a). Ao converter para acres, as unidades amostrais ficaram mais espaçadas - mais especificamente, 2,471 vezes mais espaçadas. Portanto, o desvio padrão neste caso será:
Desvio padrão em acres = 11,2 * 2,471 = 27,68 acres.
Exercício 15
Item a) São 200 as localidades com clima semitropical. Dentre estas localidades, 50 são localidades de pasto. A porcentagem de localidades com pasto, dentre as com clima semitropical, será de: (50/200) * 100% = 0,25 * 100% = 25%.
Item b) É possível notar uma coreelação entre o uso do solo e o clima. Em clima semiárido, há uma forte tendência à utilização do solo para o pasto. Já em clima semitropical, o uso do solo é majoritariamente dominado por florestas. Por fim, no clima árido, a agricultura predomina.
Com isto, concluímos que os atributos de clima e de uso do solo não são independentes.
Exercício 16
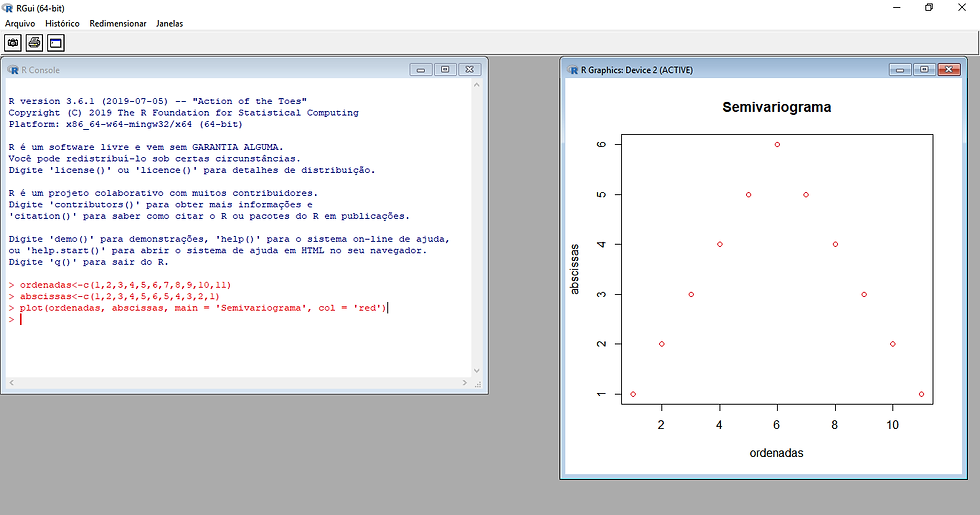
Os semivariogramas experimentais gerados em R podem ser observados nas imagens abaixo.
.png)
.png)
.png)
